
<aside> 💡
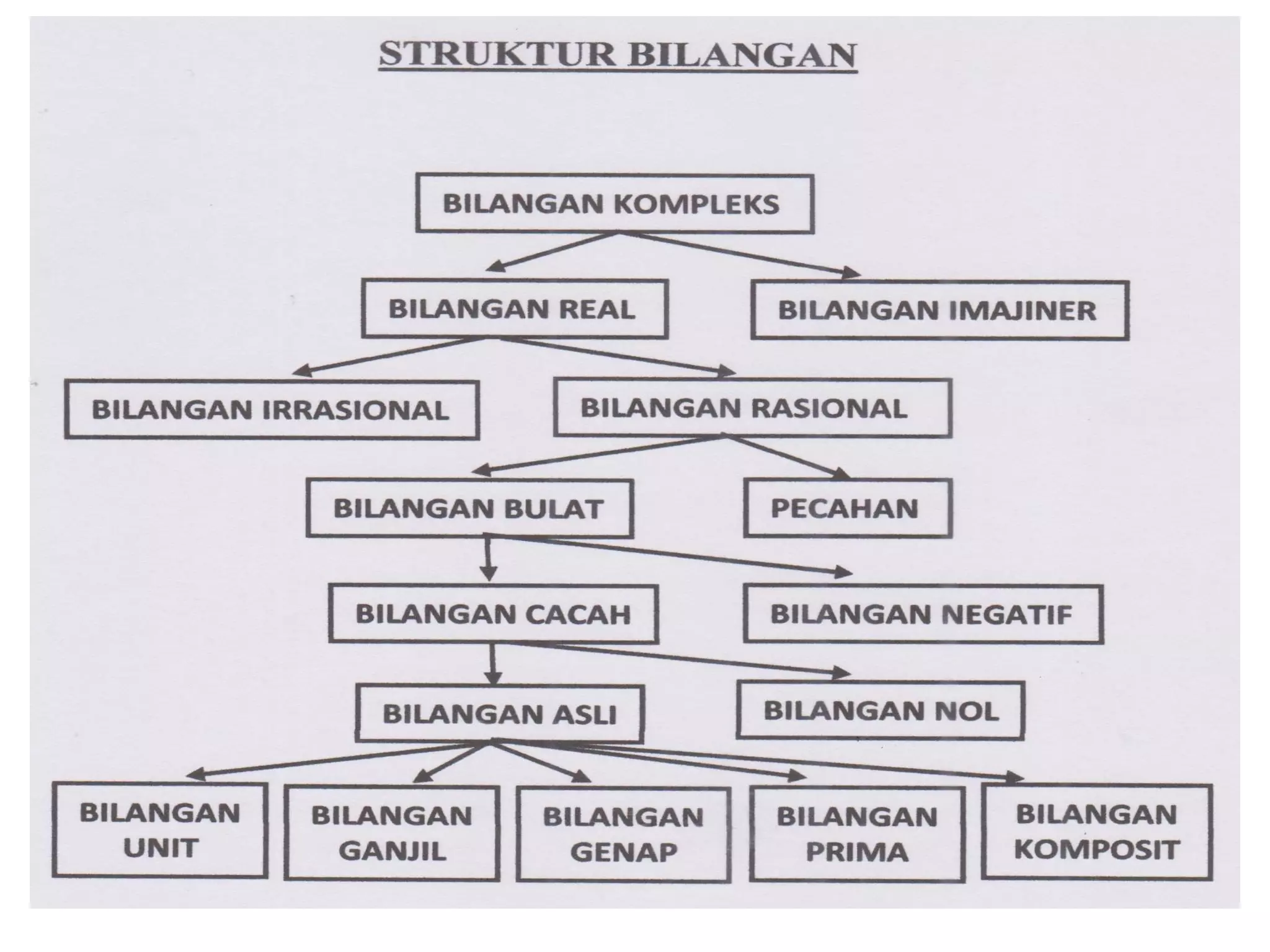
Bilangan yang dinyatakan dalam bentuk a+ib dengan a,b adalah bilangan real dan i adalah bilangan imajiner (iota).
Contoh: 2+3i, 2 adalah bilangan real dan 3i adalah bilangan imajiner.
$$ i=\sqrt{\smash[b]{-1}} $$
</aside>
a+b = a+b
-a-b = -(a+b)
a+(-b) = a-b
a-(-b) = a+b
a+0 = 0+a = a
-a+0 = 0 -a = -a
a-a = -a+a = 0
a-(-a) = a+a = 2a
Negatif X Negatif = Positif
Positif X Positif = Positif
Negatif X Positif = Negatif
Positif X Negatif = Negatif
Negatif : Negatif = Positif
Positif : Positif = Positif
Negatif : Positif = Negatif
Positif : Negatif = Negatif
<aside> 💡
Sifat Komutatif
🖊️ Operasi hitung bilangan bulat posisinya dapat ditukar dan hasilnya tetap sama.
a X b = b X a
Contoh: 3 X 4 = 4 X 3 = 12
</aside>
<aside> 💡
Sifat Asosiatif
🖊️ Operasi hitung bilangan bulat dapat dikelompokkan dan hasilnya tetap sama.
a + (b + c) = (a + b) + c
Contoh: 2 + (3 + 5) = (2 + 3) + 5 = 10
</aside>
<aside> 💡
Sifat Distributif
🖊️ Operasi hitung bilangan bulat dengan mengalikan setiap bilangan dengan bilangan yang ada dalam kurung.
a (b + c) = ab + ab
Contoh: 2 (3 + 5) = 2.3 + 2.5 = 16
</aside>
<aside> 💡
Sifat Tertutup
🖊️ Hasil operasi dari bilangan bulat selalu berupa bilangan bulat.
</aside>
<aside> 💡
Punya Unsur Identitas
a + 0= 0 + a = a
a X 1 = 1 X a = 1
Contoh: 2 + 0 = s
</aside>
<aside> 💡
Punya Unsur Invers
a + (-a) = (-a) + a = 0
Contoh: 2 + 0 = 0 + 2 = 2
</aside>